著書の思い出
| 演習で学ぶ量子力学 | 物理のための応用数学 | なっとくする複素関数 |
| 物性物理/物性化学のための 群論入門 | なっとくするベクトル | [付録] プリンキピアのトリビア |
- 『演習で学ぶ量子力学』 (裳華房, 2002)
この本は, その 10 年前に「基礎量子力学/演習」(1992) として出版されましたが, 私にとっては 殊に思い出の深いものです。 そういったことを ダラダラと 書き連ねました。
明治大学理工学部に物理学科が新設されたのは, 1988 年 (平成元年) でした。 その3年後, 1991年, 3年生に 量子力学の授業が始まりました。量子力学が 物理学科の授業の中の最難関であることは, 学生のあいだで良く知られていますが, あまり良く知られていないのが, 量子力学は 教える側にとっても難物だということです。
教務を担当していた同僚教員は, 理論系の教員の中で わずかではあるが 最年長ということで, 私に目をつけたらしく, そのお鉢が私に回ってきました。
その私はと言えば, 研究の必要上から量子力学をいろいろ学びはしたものの, これを学生に教えた経験はありません。 わずかに, 京都大学理学部で助手をしていた頃, 学生相手に演習を受け持って, シュレーディンガーの猫がどうのこうので学生を 煙 (けむ) に巻いていた程度です。
ところで, これも あまり良く知られていないことですが, 明治の物理学科のカリキュラムは, 学生向けにカッチリと組まれています。 どういうことかと言うと, 基幹科目には必ず演習が付属しており, その演習と講義とを 同一の 教員が担当します (おまけに, この2コマが連続して行なわれます。 つまり, 講義に続いて直ちに演習が行なわれます)。 物理のような学問を徹底的に学んでもらうには, この上ない理想的な方式です。
ところで, これもほとんど知られていないでしょうが, 明治の物理学科の量子力学の演習は, 何と連続2コマなのです。 つまり, 第3時限に 1 コマの講義があると, 第4, 5時限に連続した2コマの演習があり, 合計3コマで量子力学漬けとなるのです。 日の高いうちに始まった量子力学が, 冬になると, とっぷり日が暮れるまで続きます。 「月が出たのに, 量子力学演習 未だ止まぬ」という次第です。
[注:かつて 東京大学物理学科では,「力学演習 鬼か蛇 (じゃ) か, 月が出たのに未だ止まぬ」と言われたとのこと]
そして, この3コマ連続を一人の教員が担当します。 学生の人数は 60 人程度なので, クラスの大きさという点では さほど問題はありませんが, このくらいの人数だと, 質問しやすいので, 学生は遠慮容赦なく質問を浴びせてきます。
話をもとに戻すと, こういう状況で, 量子力学の講義・演習が, 私に回ってきました。
1 年間の授業です。
まず, 最低限必要なのは, 毎週 1 回の講義を 学生になるべく分かりやすくすること, そして その講義とうまく接続する2コマ分の演習問題を毎回用意することです。 これだけでも かなり大変なことです (じっさい, ホントに大変でした)。 でも, こちらも大変だということは (担当してから 身に沁みて分かったのですが)学生には なかなか分かってもらえません。考えてみればそれは当たり前のことなんですね。 だって, 学生は量子力学を理解しようと一所懸命なので, 教師の立場まですぐには理解できません。
そんな状況の中で, どうするのが最善か・・・。 そこで, 当時普及し始めたノート型パソコンの利用を思いつきました。
ここで ちょっとばかり脱線すると ・・・ 当時のノート型パソコンは CPU が漸く 80286 になったばかり, OS は MS-DOS, 液晶画面は白黒の 640×480 (後に 800×600), ところどころに (製品欠陥のため) 液晶の孔が空いていても文句を言えない ・・・ というものでした。 クロック周波数も, 現在では 数GHz が当たり前で, 中古でよければ 2万円も出せば, 立派なものが買えますが, 当時は その 1/100 程度の処理能力で, 価格が 数十万円でした。
脱線から戻ると ・・・ パソコンを使えば, 量子力学を理解してもらうのに 少しは役に立つのではないかと, 毎週 新しいプログラムをこしらえては, パソコンに入れて教室に持って行き, 演習の合間にそれを実行してもらいました。 これが どのくらい理解の助けになったかは分かりませんが, 少なくとも演習の息抜きにはなったでしょう。 何となく分かったような気がするという感想もありました。 ノート型パソコンが 個人で買うには高すぎる時代でしたから, 触ってみる 物珍しさもあったでしょう。
私としては, "観測に伴なう波束の収縮" というテーマで考えたプログラムが, なんとかうまく作成できた時点で, コンピュータ支援のこの方式が, ようやく軌道に乗ったと確信できました。
こうして書き溜めたソフトウェアと講義・演習問題を基にして, 翌年 さっそく裳華房から出版したのが本書です。
この中には, 他書には まず見られない チョーやさしい演習問題が含まれていますが, それは, こうした成立事情によるものです。
当初は, プログラムを N88-Basic で書いていたので作業効率が悪く, また, 遅い CPU では 描画に手間取って学生から好感を持たれないので, 言語好きの私は, ガンバって一部のコードをアセンブラ (機械語) で 書きました。
当時は, 浮動小数点実数の演算プロセッサ 8087 が高価だったので, 16ビットの 8086 コードを使って倍精度 (32 ビット) の浮動小数点演算を実行するという (今から見れば) ほとんど遊び (?) のようなことも しましたが, その時には, これが学生のために必須であるという気持ちで取り組んでいたように思います。
後に, CPU が Pentium になり 浮動小数点演算が自由にできるようになり, OS も MS-DOS から Windows が主流になったので, 全面的に Visual BASIC に移行しました。
それが, 「演習で学ぶ量子力学」です。
波束が ポテンシャルの山を通過する動画 (TunnelMovie) も, 今では申し分ない速さです。 Visual Basic のソースファイルもダウンロードできるようにしたので, 関心のある方は, 中身を覗いてご覧下さい。
こんな風に量子力学の担当が続き, 定年まで ずっと抜けられないのかな (笑) と半分諦めかけていたのですが, この担当は4年ほどで抜けることになりました (とは言え, 代りに降ってきたのは, 統計力学でした)。
それでも, いま ときどき思い出すのは, 夏の夕陽が教室に照りつける中, 冷房がたまたま故障で止まり汗だくだくの中で, 誰一人として文句を言う学生が無く (今では殆んど信じて頂けないでしょうが), 私が用意した演習問題に ひたすら取り組む学生さんたちを見て, 本当に頭の下がる思いをしたことです。教師としては, 実に大変な量子力学担当ではありましたが, 報われた思いがしました。 実際, そのとき 私は, 気づかれないようにではありますが (これを忘れないためにと思い) ほんの少しだけ 頭を前に傾けたので, よく記憶しています。
このあたりのことは, 工学部の物理工学科を卒業した私には, ひょっとすると理解の全く及ばないことなのかも知れません。 量子力学を学ぶのは, 確かに大変ではありますが, 見方を変えれば, これを学ぶのは 物理学科に入学した学生の特権です。他の学科に入学したのでは, 自然について これほど深く学ぶことは できません。 その誇りの気持ちが ひとりひとりの学生の心を支えているのだということに, あのとき, 深く思い至りました。
- 『物理のための応用数学』(裳華房, 1988)
これは, 3年生向けの応用数学の教科書・参考書です。
物理学科の3年生のためにどういう数学のカリキュラムを組み立てるのがよいかは, 明確な標準が ありません。
私がこの本を書くまでは, 「物理数学」と言えば, 「偏微分方程式を解く」ことを主題とする本が主流でした。
確かに, 偏微分方程式は, 物理のいろいろの分野に出てきます。
それを解くことは, 重要です。
しかし, 実際に3年生の数学の講義を担当して 講義の組み立てを考えたとき, 偏微分方程式主体では, 何とも単調で, 自分自身がその単調さにとても耐えられないだろうと感じました。
この単調さは, 学生にとっても 多分同じはずです。
自分がそんなふうでは, とても学生についてきてもらえないでしょう (と思いました)。
そこで, 自分なりの『標準』として考えたのが, この教科書です。
ただし, 実際の「物理数学」の講義では, 関数論の復習を講義の中に含めました。 また, グリーン関数 (第9章) は, 下記の事情から書き下ろしたものであり, 正規の授業には含まれていません。
また, 合流型超幾何関数 (第6章) も, 3年生全体向けには 程度が高すぎるので, 講義した記憶は ありません。ただ, 学生の中に この前書きに書いたような疑問を口にした学生が 一人だけいました。そこで, 本書執筆の際に, そのことを思い出し, この第6章を書き加えました。 そういう意味では, この章が本書に加わったのは, その学生 S 君のお蔭によるものです。あるとき (1987 年の冬), 通年の物理数学の授業が終わって, 学生たちが, グリーン関数の補講をしてほしいと言ってきました。
グリーン関数がどういうものなのか, 知りたいようです。
そこで, この本の第 9 章のような講義メモを用意して, 春休みに 十数人の学生を相手に 3 回の補講をしました。
[ 第 9 章は, 今でも時折なつかしく読み返すのですが, 学部学生のためのグリーン関数入門として, 読みやすく書かれています。 量子力学に出てくる「グリーン関数」は これとは 様子がかなり違いますが, 基本は同じです。]
それからしばらくして 6月頃に, 裳華房の編集者 (真喜屋実孜さん) がやってきて, 物理学科3年生のための数学の教科書を書くように依頼されました。
出版に携わる人は, 何か鋭い嗅覚のようなものを持っているのかも知れません。
そういう訳で, この本の執筆はトントンと進み, 夏休みの間には決定稿が出来上がり, 翌年3月に出版されました。
3年生の学生から何の得にもならない補講をしてくれと言われたのは, 約 40 年にわたる私の教員生活の中で, これ 1回だけです。 どうしてそういう話になったのかは, 今では思い出せません。
なお, 4年生からは, 次に書くように, 明治大学に移ってから, 1回だけありました。
- 『なっとくする複素関数』(講談社サイエンティフィク, 2000)
関数論 (あるいは複素関数論) は, 大学2年生で学ぶのが普通です。
複素関数論は, 大学生が学ぶいろいろな数学のなかで
(1) 大学生でも その全体を十分に理解できる
(2) 実際に役に立つ
(3) 美しい体系である(あるいは 美しさが感じられる)
という特徴があります。 多くの教科書の前書きには, そんなふうに書いてあります。
ところが, 実際に複素関数論の授業を受けている学生の感想は,
美しいどころか, ジャングルの中を歩かされているようだ ・・・
つまり, 何をやっているのか, どこへ連れて行かれるのか, 全然分からないようです。
私のこの本では, 関数論の流れを読者が ハッキリと掴むことを心がけました。
関数論が決して ジャングルではなく, 美しい一筋の流れであることを理解していただけると思います。
もちろん, ただ読むだけでは 正確な理解はできないので, 演習の問題もついていて, 実際に計算力がつくようになっています。あるとき (1999 年の6月頃, このときには私は既に明治大学の物理学科にいました), 数人の4年生が, 関数論の補講をしてほしいと言って来ました。 (大学院受験のためのようでした)。
そこで, 夏休みに入ってから, 8人程度の学生を相手に, 回数は記憶にありませんが, 厳しい暑さの中を, 関数論の 集中講義 (もちろん バッチリ その場演習つき) をしました。 8人の4年生の中には, 大学院には行かずに就職するけれども, 関数論での複雑な気持ちを払拭しておきたいから ・・・ という学生もいました。 私の研究室のゼミ生は, 8人のうちの半分くらいだったでしょうか。もともと, 私のゼミは 人気が無いのです。 (その理由はお分かりいただけると思います。)
その集中講義で, たまたま「複素関数の微分可能」の意味を (おそらく 必死になって(笑)) 説明しているときに, 私の講義ノートには書かれていない 超なめらかという言葉が, 思わず私の口を突いて出たのです。 それも, たまたま, あの I 君が私に向けた目に「先生, そんなんじゃ 未だ分からないよ」というような表情を感じた時の咄嗟の出来事でした。
超なめらか というのは, その場で思いついた自家製の数学用語でしたが, 複素関数の性質を感覚的にうまく伝えるキーワードです。
それから数ヵ月後 (1999 年11月), 講談社の末武親一郎さんが 飛び込みで (誰の紹介も無しに) やって来られました。 「なっとくする複素関数」をぜひ書いてほしい, という依頼でした。
本が生まれるときには, いくつかの偶然が重なるものです。
そういうわけで, この本もスラスラと進み, 翌年 春 (2000 年4月) に出版されました。
もちろん, 末武さんご自身が 夏の「補講」を嗅ぎつけて来られたわけではありません。 そのとき 手にしておられたのが, 私が その 12 年前に付録として書いておいた 7ページの付録「関数論入門」でした。 あれを膨らませて 1 冊の本にしてほしい。 ただし「論」を省いてほしい ・・・ それが, ご希望の全部でした。後から分かったことですが, この本の編集あたりを最後に, 末武さんは 講談社を定年退職なさったようです。 それだけに, この本に注ぐ熱意は並大抵ではなく, ほとんど毎週 1 回の定期便と言ってよいくらい, 実に細かいところまで疑問を指摘してこられました。 それにいちいち呼応する形で, 私は, これで どうでしょうか ・・・ と 改稿を重ねました。
かなり後にうかがったところでは, 末武さんは あの有名な "ブルーバックス・シリーズ" の屋台骨を担っておられた講談社の重鎮編集者とのことで, このような方に 定年前最後のお仕事として 私の原稿をお読みいただいたことを 物書きとして, 大変うれしく思います。
ちょっと脱線すると, この本の中には, 割り込みチャイム という仕掛けが用意されていて, 読者が つまづきそうになると, 私自身が大学生だった頃に疑問に感じたことを 著者にストレートにぶつける仕掛けになっています。ときどき, あれは 「なっとくする シリーズの標準メニューなのか?」とお尋ねをいただきます。あのチャイムの「ピンポーン」は, 我が家の玄関のチャイムの音をそのまま採用しました。 こどもたち (とくに 娘) が帰宅すると, あの音色のチャイムが鳴るので,「これだっ!」と思いつきました。
ただ, いま振り返ってみると, あのチャイムは, 末武さんも かなり鳴らしておられたのです。本の束
今 これを書きながら, 末武さんとのやり取りの中で, "本の束 (つか)" という術語を教えられたことを思い出した。
束とは, 本の厚さを意味するらしい。
本書の目的から考えれば, この程度が 厚すぎもせず, 薄すぎもせず ちょうど良いと 私は 考えたのですが, 「なっとくシリーズ」の他書より明らかに薄い。 平積みにして売れる本ではないので, 「書店の書棚に縦に並べると, 痩せて見える, 背文字が小さな文字になる ので損をする, 売れ行きに影響するかも・・・」 ということなのでした。 自分の想定外だったので, これには 驚きを覚えました。
結局どうしたかというと, 無理に厚くしても意味は無いし, 読者も 数学の本まるまる 1冊を読んだという満足感が得られるだろうから ・・・ ということで, 納得していただきました。
- 「物性物理/物性化学のための 群論入門」(裳華房, 1996)
本書は, 群論を必要とする実験家を読者対象として, 書かれた入門書です。
群論というのは, 数学の一分野であるだけに, これを正確に身に付けようとすれば, 物理側から見たときの敷居の高さは, かなりのものです。 しかし, そういうことで 手間取っていては, 現場の役に すぐには 立ちません。
一方では, 化学の立場から群論への入門を容易にする企てが, 必要上 いくつもなされてきました。
しかし, 物理側から見た場合, それらの (化学からの) 入門書は, 基礎的な説明が全く不十分であり, 「納得した上で使いこなす」 ことができません。
別段 ここで (高校生のときから好きだった) 化学の悪口を言い立てるつもりはありませんが, 私が見る限り, 化学の本というのは, そこに書かれていることをそのまま使える場合には, 非常に役に立ちます。しかし, そこから一歩でも外れて応用する ・・・ となると, 途方に暮れる ・・・ そういうことが多いのです。 或る意味では, これは 化学という学問の性質上 やむを得ないことです。
一般に 物理屋さんは, 理屈が好きだと言われます。 それは, 確かにその通りです。
また, 一般に 物理屋さんは,「数学を使って厳密に論理を進めれば, 100 % 落ちる」と思う人がいるようです。けれども, こちらの方は 完全な誤解です。そんなことで 物理が理解できるのだったら, 力学の講義も電磁気学の講義も, 教える側の苦労は ありません。
物理を専門とする人は, (かつて 力学, 電磁気学, 熱力学などを学んだ経験から) 基礎概念を把握した上でないと応用に進めない ・・・ これは, 物理屋の欠点でもあると同時に, 長所でもあります。
長々と書き立てましたが, 要するに, なるべく基礎的なところを はしょらずに, しかも なるべく早く 読者にとって必要な応用力を身に付ける ・・・ ということを目標としたのが, 本書です。
この目的がどの程度果たされたかは, 読者の判断を待つしかありません。
Web で検索すると, 大学院の講義で参考書 あるいは テキストとして取り上げられているようです。 また, 大学院修士課程 あるいは 卒業研究の学部学生のゼミにテキストとして使われているようです。少数であっても, このような使われ方をしているのであれば, 著者として その目的を果たし, 努力が報われたように感じます。「定年になって時間ができたら, 本を書こう」という人は, 何人も おられます。しかし, 定年を迎えると, 本を書く気力も同時に失せる ・・・ というのが 現実です。おまけに, 既に講義をしていない定年教授に本を書いてもらっても 売れないので, 出版社は喜びません。本というのは, やはり, 定年前の 忙しい時期にこそ, 生きた講義をしている最中にこそ 書くべきものです。
以上は, これから本を書こうと お考えの 私より若い方々のために, 老婆心から書き留めました。
そういう目で いま 自分自身を振り返ってみると, 不満を感じることは ありません。これは, 本を書く立場として 幸せなことなのでしょう。書き残したと思うことは, ほとんど ありません。
一方で, インターネットが普及したこの時代には, 本の評判を直接に知ることができる ・・・ という楽しみがあります。書評というものは, かつては, その筋の権威ある人が書いたものしか読めなかったのが, いまでは, 言わば素人読者の書評まで含めて, いろんな感想を知ることができます。 これは, 定年後の私にとって, 大きな楽しみです。 ときには, 思っても見なかった反響に, こちらがビックリすることがあり, それがまた楽しみでもあります。
- 『なっとくするベクトル』(講談社サイエンティフィク, 2001)
"なっとくする複素関数" の翌年, 大学新入生のためにと思って書いたのが, "なっとくするベクトル" です。
はじまり
前著 "複素関数" が順調に上梓されて 未だ 私の手許に届かぬ間に, 末武さんから 次は "ベクトル解析" を考えてもらえないか ・・・ との ご依頼がありました。
これについて 私の答は, "ベクトル解析" には 少ないながらも良書があり, また, "ベクトル" を "解析" まで必要とするのは, "物理" と "機械" の学生であって, 需要は かなり少ない筈だというものでした。
それに, "複素関数" の場合にも, 高等学校で習った筈の "複素数" の演算を まともにできない大学生が 余りにも多く, そのために1章を割く必要がありました。 "ベクトル" についても同様で, いかに 高等学校で既習とは言え, 理工系大学生の "ベクトル" 処理能力がどの程度であるかは, 力学の講義担当者には よく知られたことです。
そういうわけで, "ベクトル解析" の前座として, むしろ "ベクトル" が 必要だろう ・・・ ということから 本書が生まれました。
いまでは 品切れ
2001年4月に発売された本書ですが, 2014年4月には, 講談社で本書の編集の実質的な お仕事をして下さった大塚記央さんから E-メールが届き, 本書は 品切れのまま (事実上 絶版) となりました。
13 年の いのち でした。手許の記録を調べてみると, 発行部数は 第4刷までで 6,000 部となっています。学生が本を買わない傾向がますます強くなっているので, 絶版も止むを得ないでしょう。
もっとも, アマゾンを見に行くと, 新本同様の古本に 定価の倍の値がついていて, 実に 割り切れないものを感じます(笑)。古本の値打ちは, (たとえ誤植があっても) 初版のものが 最高なのだそうです。
もちろん, 特別の人を除いて こんな高値の本を買う必要はありません。 理工系の大学学部ならば, 図書館で購入されているはずです。 この本は, 基本的には, 大学新入生が 力学の授業で ベクトル (および 微積分) で困ったときの助けになるように書いたものなので, 必要な学生さんは, 図書館でお読み下さい。
ニュートン (1643/1/4 - 1727/3/31)
ここで, 話の風向きを変えよう。
本書は 力学を正面から扱っているわけではないが, それでも ニュートンが ところどころに顔を出す。
この扱いをどうすればよいのか, 判断に 少し迷った。 結局のところ, ベクトルを主戦場にするという理由から, 運動の3法則 (ニュートン自身は これを "公理, あるいは 運動の法則" と呼んでいる) については, ほとんど説明しなかった。新入生向けの力学の講義でも, これを 公理として 神棚に上げておく方が, 安全だろう。
そういう "安全策" を取ったのであるが, やはり不満は残った。こんな 小さな本でも, ニュートンの雰囲気を少しでも 大学新入生に伝えたい … という気持ちが 残る。 そこで, "中心力場では, 面積速度が一定に保たれる" というニュートンの証明を取り込んだ。 これは, 高校生程度の 平面幾何と物理の知識があれば, 容易に理解できる。
本書が 絶版になってしまったので, その図を新たに描き直し, ここに採録することにした。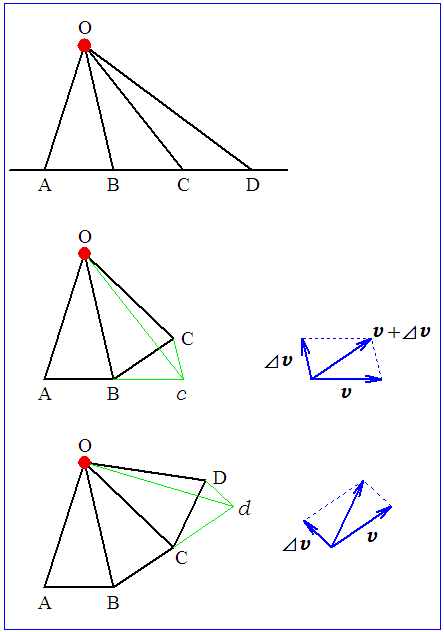
この図を見るだけで 全てを理解する人は 多いだろうが, 念のために説明を加える。
ニュートンの議論の要点は, 時間を 細かい等間隔 ⊿t で区切って考えることだ。 もちろん, 最終的には ⊿t を無限小の時間 dt に移行させる。
(1) はじめに 太陽 O と地球の間に引力が働かないとする。 このとき, 地球は一定速度で A → B → C → D → ・・・ と進む。 次々に作られる三角形の面積は等しいから, 面積速度 (面積の増加率) は一定である。
(2) 次に, 太陽と地球の間に 中心力が 働くとする (逆2乗則である必要はない)。 力は つねに 働いているのだが, ニュートンは, 力として撃力を考える。 つまり, ⊿t ごとに 太陽方向の撃力が 地球に瞬間的に加わり, それ以外の時間は 第1法則に従う (速度一定の) 運動をすると考える。
一定速度 v で A から B まで走った地球は, B 点で 太陽方向の撃力を受け, その結果 太陽方向の速度成分 ⊿v を得て 軌道を曲げられ, 時間 ⊿t 後に C 点に到る。 もしも引力が無ければ, 地球は 同じ時刻に c 点に到達する。 ここで 三角形 ⊿OBC と三角形 ⊿OBc は, 面積が等しい。 なぜなら, 中心力の要請により Cc が OB に平行だからである。
こうして, 次々に作られる三角形の面積が すべて等しいことが証明できる。

プリンキピアのトリヴィア
右は, 1686年7月5日の日付がついた プリンキピア 第1版 (1687 年出版) のタイトル・ページである。 大文字の部分だけを拾って読むと "Philosophiae Principia (哲学の諸原理)" となっている。 その理由については, 諸説があるらしい (Halley が決めたとか, 印刷工が見栄えを重視したとか, デカルトが どうこうとか)。
このタイトル・ページを額に入れて飾ったものを, 誰が買うのか知らないが Amazon.co.uk は, £56.25 (~¥8,300) で売っている。
1726年の第3版 (右) は, ニュートン存命中の最後の版であるが, ここでは, 大文字部分が 赤インクで印刷されて, さらに強調されている。 つまり, プリンキピア 第3版は, タイトルページに関する限り, 2色刷りだったのだ。 ここからは, ニュートンが "哲学の原理" であることを強調したかった印象を受ける。 ただし, このように赤インクをタイトル・ページに使うことは, 他にも見えるから, さほど特別のことではなかったのかもしれない。
この第3版のファクシミリ版が, 1972 年にハーバード大学出版局から出ている。 お値段は $150 である。額縁の 2倍チョット。 記念に買ってあれこれ楽しむなら, こちらが 良いでしょうか ・・・。
プリンキピアの現代英語訳は, 1999年に カリフォルニア大学出版局から出た I. B. Cohen & Anne Whitman によるものが 決定版とされているが (¥6,874), その長文の解説を読むと, 驚いたことに, 現代の英語読者が読める まともな英語訳は, 長いあいだ 不在であったという。
1999 年より前の完全訳は, Andrew Mott (1726) によるもので, それを Florian Cajori が 1930 年代に改訂して (1934), これが 標準とされてきた。
ラテン語ファクシミリ版を出版した際に, このような 時代遅れの英語訳の 誤解を招きやすい点については注釈をつけておいたが, そういう古い訳が 正しいかどうかを説明するよりは, 自分たちで 新訳を出してくれ ・・・ という強い声があったので, 新しい翻訳をせざるを得なかった と Cohen は書いている。
そう書いてあるのを読んで, ハタと思い当たる感じがした。これまで, 力学の講義をするとき, "公理, あるいは 運動の法則" を 基本的には "公理" として 神棚に上げる安全策を採用してきた私であるが, やはり 神棚の中身は気に掛かる。 ニュートンが 結局のところどういうことを言っているのか (質量とは何か, 慣性とは何か, "チカラ" というものを どう考えていたのか, 作用とチカラは 同じなのか違うのか ・・・ などなど) 気に掛かり, そのときに読んでいたのは, 大抵は Cajori による英語訳だった。
という訳で, もしも 筆者と同じような 隔靴掻痒感を経験なさった方がおられるならば, Cohen & Whitman 訳をお勧めしたい。 力学の講義をなさるときの気持ちに いくらか整理がつくかも知れない。
ただし ・・・, それで 全てがスッキリするというわけではない。 確かに, 正しく理解できることがあるが, 同時に分からないことが増える。 これは, 世の中の常である。
