　
内容見本タイトル

著作者紹介

浦川　肇
うらかわはじめ
1946年兵庫県生まれ．東北大学理学部卒業，大阪大学大学院理学研究科修士課程修了．名古屋大学助手，東北大学助教授，マックス・プランク数学研究所客員教授，東北大学教授などを歴任．主な著書に『ラプラシアンの幾何と有限要素法』『微積分の基礎』（以上朝倉書店）などがある．

（情報は初版刊行時のものから一部修正しています）

【電子書籍】
変分法と調和写像
Calculus of Variations and Harmonic Maps

東北大学名誉教授　理博　浦川　肇著

標準価格5060円（本体4600円＋税10％）／2016年7月電子版発行／
eISBN 978-4-7853-7111-1

　理工系学生にとって重要な「変分法」と応用編である「調和写像」(場の理論）は近年，めざましい発展を遂げ，自然科学において必須の分野となりつつある．これらの理論の発展の様子を，その基礎から初学者向けに丁寧に解説したものが本書である．
　４章以降の応用編のみを切り離しても読み進められるように配慮されている．

※この電子書籍は固定レイアウト型で配信されております．固定レイアウト型は文字だけを拡大することや，文字列のハイライト，検索，辞書の参照，引用などの機能が使用できません．
※この電子書籍は，2014年に刊行された『変分法と調和写像』（第3版5刷）を元に電子書籍化したものです．

サポート情報

◎ “紙”の書籍の紹介ページは→こちら
◎ 序文（pdfファイル）　　 ◎ 索引（pdfファイル）

目次（章タイトル）　　→ 詳細目次

1．変分法
2．多様体
3．モース理論
4．調和写像
5．第２変分公式と安定性
6．調和写像の存在・構成・分類

詳細目次　　→

序文（pdfファイル）

1．変分法
　1.1　本書の目標
　1.2　変分法と場の理論
　1.3　変分法の例
　1.4　反省と今後の指針
　ティー・タイム　古典力学と変分法

2．多様体
　2.1　連続性と微分積分
　2.2　$C^k$ 多様体
　2.3　有限次元 $C^∞$ 多様体
　2.4　多様体の例

3．モース理論
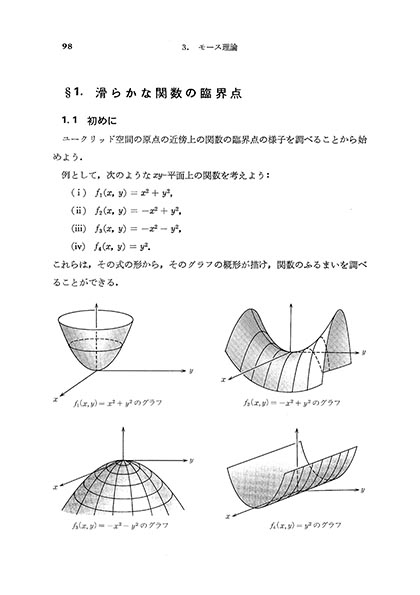
　3.1　滑らかな関数の臨界点
　3.2　滑らかな関数の最小値
　3.3　条件（C）
　3.4　応用
　ティー・タイム　等周問題とディドー女王

4．調和写像
　4.1　調和写像とは
　4.2　第１変分公式の別の表示
　4.3　調和写像の例
　ティー・タイム　石けん膜と極小曲面（プラトー問題）

5．第２変分公式と安定性
　5.1　第２変分公式
　5.2　不安定性定理
　5.3　正則写像の安定性

6．調和写像の存在・構成・分類
　6.1　存在・構成・分類の問題
　6.2　球面の場合
　6.3　対称空間のとき
　6.4　変分法による存在証明法

問題解答
参考書
索引