|



※POD版のご注文は、お近くの書店・大学生協書籍部、または直接 弊社にお願いします。
※受注生産のため、ご注文されてからお手元に届くまでに時間がかかります(通常 半月程度)。
※ご注文の取り消し・キャンセル、またご注文商品の返品は一切できません。
※以上 あらかじめご了承の上、ご注文くださいますようお願いいたします。

・Amazon Kindleストア
・楽天Kobo
・Google Play
・BOOK☆WALKER
・BookLive!
・紀伊國屋 kinoppy
・セブンネットショッピング
・Reader Store
・ひかりTVブック
・honto
・eBookJapan
・dブック
・どこでも読書
・いつでも書店
・COCORO BOOKS
・auブックパス
・DMM電子書籍

|
|

名古屋大学名誉教授 理博 栗田 稔 著
A5判/218頁/定価3960円(本体3600円+税10%)/
1974年10月発行,復刊 2002年8月発行,POD版 2019年8月発行
ISBN 978-4-7853-0644-1 C3041
(オリジナル版ISBN 978-4-7853-1111-7,旧ISBN 4-7853-1111-8)

本書では、まず直線上の座標からデカルト座標、直角座標に進み、転じて極座標,さらに一般の曲線座標におよび、最後に射影幾何学における射影座標で結んでいる。
特に留意した点は、以下の通りである。
(1)現代の数学では、デカルト座標、直角座標はベクトルを基本として考えていくことが自然で、本書でも2次元、3次元のベクトルについては詳述している。
(2)3次元のベクトルを扱うのには行列式が不可欠であるが、これに関する知識で、本文で利用していることについては、補充として巻末に示している。
(3)曲線座標については紹介する程度に止めた。
(4)扱う例や問題は在来のものに加え、新鮮味のあるものを採り入れた。
※オンデマンド出版書籍(POD版;オンデマンド版)は出版物をデジタルデータ化して、1冊から印刷・製本・販売を行う書籍です。
サポート情報
◎ まえがき (pdfファイル)
◎ 索引 (pdfファイル)
1.座標の概念
2.直線上の座標
3.ベクトルとデカルト座標
4.直角座標
5.極座標
6.曲線座標
7.射影座標
まえがき (pdfファイル)
1.座標の概念
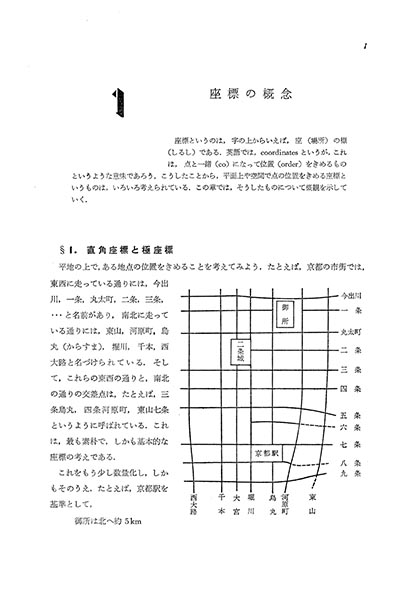
1.1 直角座標と極座標
1.2 デカルト座標
1.3 空間での座標
1.4 曲線座標
1.5 射影座標
1.6 座標と図形
1.7 多次元空間の座標
2.直線上の座標
2.1 有向線分の長さ
2.2 座標
2.3 座標の変換と点の変換
2.3.1 原点を変えるとき
2.3.2 原点や正負の向きは変えないで,単位の長さを変えるとき
2.3.3 原点や単位の長さは変えないで,正負の向きを変えるとき
3.ベクトルとデカルト座標
3.1 べクトル
3.2 位置ベクトル
3.3 ベクトルの成分(平面)
3.4 デカルト座標(平面)
3.5 ベクトルの成分(空間)
3.6 デカルト座標(空間)
3.7 座標の変換と点の変換
4.直角座標
4.1 べクトルの直角成分と直角座標
4.2 内積
4.3 平面上の直線の方程式
4.4 円周
4.5 円錐曲線
4.6 不等式と領域
4.7 外積
4.8 空間図形の方程式
4.9 座標軸の回転と2次曲線の分類
4.10 座標軸の回転(空間)
4.11 合同変換
5.極座標
5.1 平面上の極座標
5.2 極方程式
5.3 直角座標から極座標へ
5.4 複素平面
5.5 空間の極座標
6.曲線座標
6.1 平面上の曲線座標
6.2 曲線座標での長さと面積
6.3 曲面上の曲線座標
6.4 空間の曲線座標
7.射影座標
7.1 無限遠点
7.2 射影直線
7.3 射影平面
7.4 点と直線の双対
7.5 2次曲線
補充 行列式
2次の行列式
3次の行列式
行列式の積
索引 (pdfファイル)
|
|

栗田 稔
くりた みのる
1913年 静岡県に生まれる。東京帝国大学理学部卒業。旧制第八高等学校教授、名古屋大学教授などを歴任。主な著書に『積分幾何学』(共立出版)、『リーマン幾何』(至文堂)、『現代幾何学』(筑摩書房)、『微分形式とその応用』(現代数学社)などがある。
(情報は初版刊行時のものから一部修正しています)


平面幾何学

立体解析幾何学

初等幾何学

幾何概論










|
