|



Amazon
楽天ブックス
セブンネットショッピング
Knowledge Worker
紀伊國屋書店
ヨドバシ・ドット・コム
ローチケHMV
e-hon
Honya Club

丸善,ジュンク堂書店,文教堂
紀伊國屋書店(新宿本店)
三省堂書店
有隣堂
くまざわ書店
コーチャンフォー


|
|

東京大学名誉教授 理博 三村征雄 編/
東京大学名誉教授 理博 三村征雄・
元東京大学教授 理博 田村二郎・
東京大学名誉教授 理博 新納文雄・
東京大学名誉教授 理博 岩堀長慶・
一橋大学名誉教授 理博 松坂和夫 執筆
A5判/398頁/定価4730円(本体4300円+税10%)/1955年2月発行
ISBN 978-4-7853-8001-4 (旧ISBN 4-7853-8001-2)
C3041
(オンデマンド方式による印刷・製本)
大学基礎課程における微分積分学を学ぶ人たちのために標準的な問題とその解法を示した。
まず基本的事項を明確に説き、適切な例題によって解法の規範を与えた後、練習問題を難易によりA、B、Cの三段階に分けて系統的に叙述し、すべての問題に詳細なる解答を付している。
第I部 基本概念
1.実数とその函数
2.数列
3.函数の極限とその連続性
第II部 導函数
1.微分法
2.導函数の性質とその応用
3.点の運動と曲線
第III部 積分
1.積分の概念
2.初等函数の積分法
3.定積分
4.定積分の応用
第IV部 級数
1.級数の収斂と発散
2.羃級数
第V部 偏導函数
1.多変数の函数
2.偏微分法
3.偏導函数の応用
4.曲線と曲面
第VI部 重積分
第VII部 微分方程式
1.求積法によって解ける一階微分方程式
2.線型微分方程式
附録 極限に関する基本事項の証明
序/凡例
第I部 基本概念
§1.実数とその函数
1 実数の集合
2 変数と函数
3 函数の例
例題
問題
解答
§2.数列
1 数列の極限
2 極限の性質
例題
問題
解答
§3.函数の極限とその連続性
1 函数の極限
2 無限小
3 函数の連続性
4 連続函数の性質
5 指数函数と対数函数
例題
問題
解答
第II部 導函数
§1.微分法
1 導函数の定義
2 微分法の公式
3 基本的な函数の導函数
例題
問題
解答
§2.導函数の性質とその応用
1 平均値の定理と函数の増減
2 Taylorの定理と函数の近似値
3 最大最小と極大極小
4 凸函数
5 不定形の極限値
例題
問題
解答
§3.点の運動と曲線
1 ベクトルの概念とその代数的演算
2 ベクトルの連続性とその微分法
3 空間における点の運動と連続曲線
4 平面曲線
5 特殊平面曲線
例題
問題
解答
第III部 積分
§1.積分の概念
1 定積分の定義
2 定積分の性質
3 原始函数(不定積分),微分積分法の基本公式
4 不定積分の基本公式
5 置換積分法と部分積分法
例題
問題
解答
§2.初等函数の積分法
1 有理函数の積分
2 無理函数の積分
3 初等超越函数の積分
例題
問題
解答
§3.定積分
1 定積分の計算
2 定積分の近似計算(Simpsonの公式)
3 定積分の定義の拡張(広義の積分)
4 広義の積分の収斂条件
例題
問題
解答
§4.定積分の応用
1 面積
2 曲線の長さ
3 回転体の表面積および体積
4 平均値,重心,慣性能率
例題
問題
解答
第IV部 級数
§1.級数の収斂と発散
1 級数の和
2 正項級数
3 交項級数
4 絶対収斂
例題
問題
解答
§2.羃級数
1 羃級数の収斂半径
2 羃級数の性質
3 函数の展開
4 基本函数の展開式
例題
問題
解答
第V部 偏導函数
§1.多変数の函数
1 数平面
2 開集合と領域
3 閉集合と有界集合
4 二変数の函数
5 函数の極限値
6 連続函数
7 $n$ 変数の函数
例題
問題
解答
§2.偏微分法
1 偏導函数
2 全微分
3 接平面
4 高次偏導函数
5 合成函数の偏微分法
6 Taylorの定理と平均値の定理
例題
問題
解答
§3.偏導函数の応用
1 極値
2 陰函数
3 条件付き極値問題,Lagrangeの未定乗数法
4 写像
例題
問題
解答
§4.曲線と曲面
1 平面曲線の追跡
2 曲面
3 包絡線と包絡面
例題
問題
解答
第VI部 重積分
1 二重積分の定義と面積
2 積分の性質
3 三重積分
4 変数の変換
5 面積,体積および曲面積
6 線積分と面積分
7 物理学への応用
例題
問題
解答
第VII部 微分方程式
§1.求積法によって解ける一階微分方程式
1 平面曲線群の微分方程式を作ること
2 空間曲線群の微分方程式を作ること(連立微分方程式)
3 存在定理および解の一意性
4 一般解,特殊解,特異解
5 変数分離形
6 同次形
7 同次形の拡張
8 一階線型微分方程式
9 完全微分形
例題
問題
解答
§2.線型微分方程式
1 線型微分方程式
2 基本解
3 階段を下げること
4 定数変化法
5 定数係数の線型微分方程式(斉次の場合)
6 定数係数の線型微分方程式(非斉次の場合)
7 特殊解を求めるその他の方法
例題
問題
解答
附録 極限に関する基本事項の証明
1.数列の極限
2.極限の存在定理と実数の連続性
3.上極限と下極限
4.函数の極限
5.連続函数の性質
6.函数の一様連続性
7.函数列の一様収斂
8.Riemann積分とDarboux上積分,下積分
索引
|
|

三村 征雄
みむら ゆきお
1904年 東京都に生まれる。東京帝国大学理学部卒業。東京大学教授などを歴任。1984年逝去。主な著書に『微分積分学 I』『微分積分学 II』(以上 岩波書店)、『ヒルベルト空間論』(春日書房)などがある。
田村 二郎
たむら じろう
1920年 大阪府に生まれる。東京帝国大学理学部卒業。旧制第一高等学校講師、東京大学教授・学部長などを歴任。主な著書に『空間と時間の数学』(岩波書店)、『量と数の理論』(日本評論社)などがある。
新納 文雄
にいろ ふみお
1923年 神奈川県に生まれる。東京帝国大学理学部卒業。旧制第一高等学校講師、東京大学講師・助教授・教授などを歴任。2002年逝去。
岩堀 長慶
いわほり ながよし
1926年 東京都に生まれる。東京大学理学部卒業。東京大学助教授・教授、上智大学教授などを歴任。2011年逝去。主な著書に『2次行列の世界』(岩波書店)、『初学者のための合同変換群の話』(現代数学社)などがある。
松坂 和夫
まつざか かずお
1927年 兵庫県に生まれる。東京大学理学部卒業。東京大学助手、武蔵大学助教授、津田塾大学助教授、一橋大学教授などを歴任。2012年逝去。主な著書に『解析入門(全6巻)』『数学読本(全6巻)』『代数への出発』(以上 岩波書店)などがある。
(情報は初版刊行時のものから一部修正しています)


解析関数(新版)

大学演習
代数学と幾何学


問題集 微分積分

微分積分演習

基礎演習シリーズ
微分積分

微分積分 主要教科書一覧
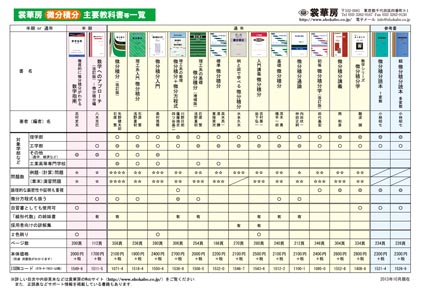
(2013年10月作成,pdfファイル)











|
