Amazon
楽天ブックス
セブンネットショッピング
Knowledge Worker
紀伊國屋書店
ヨドバシ・ドット・コム
TSUTAYA
ローチケHMV
e-hon
Honya Club

丸善，ジュンク堂書店，文教堂
紀伊國屋書店（新宿本店）
三省堂書店
有隣堂
TSUTAYA
くまざわ書店
コーチャンフォー

数学へのアプローチ（改訂版）−微分積分編−
An Approach to College Mathematics 2nd edition −Calculus−

京都府立医科大学名誉教授　Ph.D.　八木克巳 著

Ａ５判／112頁／定価1870円（本体1700円＋税10％）／1998年11月発行
ISBN 978-4-7853-1511-5 （旧ISBN 4-7853-1511-3）　 C3041

　半年間の講義で学べるように内容を絞って解説した入門書．各テーマごとに，１変数と２変数の関数を平行に取り扱う方針をとり，高校で学ぶ微分積分との違いを最初から感じとれるように配慮し，理解を助ける工夫をした図も多用してある．
　姉妹書に『数学へのアプローチ（改訂版）−線形代数編−』がある．

サポート情報

◎ はじめに （pdfファイル）　　
◎ 正誤表 （pdfファイル）

目次 （章タイトル）　　→ 詳細目次

1．関数
2．微分
3．微分の計算
4．増減表
5．２次関数による近似
6．変数変換
7．積分の定義
8．定積分の計算
9．重積分の計算
10．Taylor級数
11．微分方程式

詳細目次　　→

はじめに （pdfファイル）

1．関数
　1.1　１変数の関数
　1.2　２変数の関数

2．微分
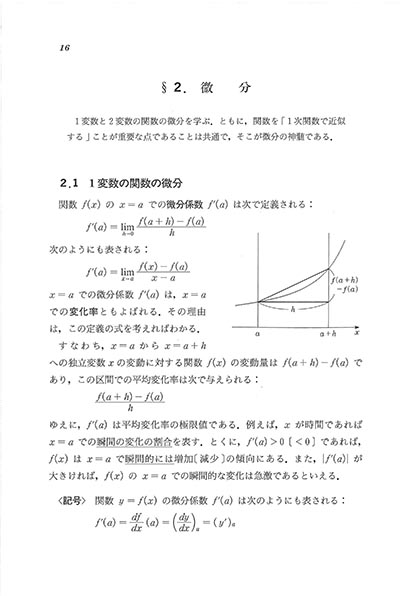
　2.1　１変数の関数の微分
　2.2　２変数の関数の微分

3．微分の計算
　3.1　基本的な性質
　3.2　初等関数の微分
　3.3　高次微分，高次導関数

4．増減表
　4.1　１変数の関数の増減表
　4.2　２変数の関数のgradient

5．２次関数による近似
　5.1　１変数の関数の２次関数による近似
　5.2　２変数の関数の２次関数による近似

6．変数変換
　6.1　１変数での変数変換の例
　6.2　変換
　6.3　Jacobi行列

7．積分の定義
　7.1　定積分
　7.2　重積分の定義

8．定積分の計算
　8.1　微積分学の基本定理
　8.2　不定積分
　8.3　定積分の応用
　8.4　「微積分学の基本定理」の再考

9．重積分の計算
　9.1　累次積分
　9.2　極座標による変数変換
　9.3　一般の変数変換

10．Taylor級数
　10.1　１変数の $n$ 次関数による近似
　10.2　Taylor級数

11．微分方程式
　11.1　微分方程式
　11.2　１階微分方程式
　11.3　２階線形微分方程式

付録　「線形代数」のまとめ
演習問題略解
索引

八木 克巳
やぎ かつみ
1965年 大阪大学理学部卒業．米国Notre Dame大学にて Ph.D 取得．大阪大学講師・助教授，京都府立医科大学教授などを歴任．専門は微分幾何学，統計学．

（情報は初版刊行時のものから一部修正しています）

数学へのアプローチ
（改訂版）
−線形代数編−

微分積分通論


徹底的に微分積分がわかる
数学指南


微分積分（改訂版）

微分積分 主要教科書一覧

（2013年10月作成，pdfファイル）