|





Amazon
楽天ブックス
セブンネットショッピング
Knowledge Worker
紀伊國屋書店
ヨドバシ・ドット・コム
ローチケHMV
e-hon
Honya Club
ブックサービス

丸善,ジュンク堂書店,文教堂
紀伊國屋書店(新宿本店)
三省堂書店
有隣堂
くまざわ書店
コーチャンフォー


|
|
微分法&積分法
Calculus

名城大学教授 理博 江尻典雄・
名古屋大学名誉教授 理博 三宅正武 共著
A5判/288頁/定価2750円(本体2500円+税10%)/1999年11月発行
ISBN 978-4-7853-1519-1 (旧ISBN 4-7853-1519-9)
C3041
大学理工系向きに題材を選び,前半は微分法(1変数および多変数),後半は積分法(1変数および多変数)の構成でまとめた教科書.カリキュラムによっては,1変数の微分と積分を前半に,多変数の微分と積分を後半に学ぶこともできる.
高校課程の数学IIIを学んでこなかった読者にも理解できるように,実数の性質や数列の極限および収束性についての解説は付録にまわして,微分法の最初に述べる連続関数から直接的に微分法・積分法の本論に入れるように解説した.連続関数の積分可能性の証明を含め,理論面も軽視せず解説してある.
サポート情報
◎ まえがき (pdfファイル)
◎ 正誤表 (pdfファイル)
● 微分法
1.1変数連続関数
2.1変数関数の微分
3.テイラーの定理(1)
4.多変数関数
5.多変数関数の微分
6.テイラーの定理(2)
7.陰関数定理
● 積分法
8.1変数関数の積分
9.積分の計算
10.広義積分とベータ関数,ガンマ関数
11.積分の応用
12.多変数積分法
13.重積分における変数変換
14.線積分とグリーンの定理
まえがき (pdfファイル)
● 微分法
1.1変数連続関数
1.1 初等関数
1.2 関数の演算,合成関数,逆関数
1.3 連続関数
1.4 連続関数の性質
2.1変数関数の微分
2.1 微分可能性
2.2 初等関数の導関数
2.3 合成関数の導関数
2.4 逆関数の微分
2.5 高次導関数
3.テイラーの定理(1)
3.1 ロルの定理
3.2 平均値の定理
3.3 テイラーの定理
3.4 応用
3.5 凸関数
4.多変数関数
4.1 多変数関数
4.2 極限値
4.3 連続関数
4.4 連続関数の性質
5.多変数関数の微分
5.1 方向微分,偏微分
5.2 $C^1$ 級関数の性質
5.3 グラフの接平面
5.4 合成関数の微分
5.5 高次偏導関数
6.テイラーの定理(2)
6.1 平均値の定理の一般化
6.2 極値問題
7.陰関数定理
7.1 陰関数定理
7.2 ラグランジェの未定乗数法
● 積分法
8.1変数関数の積分
8.1 微積分の基本定理
8.2 リーマン和と定積分
8.3 原始関数と定積分
8.4 定積分の基本性質
8.5 広義積分
9.積分の計算
9.1 部分積分法
9.2 置換積分法
9.3 有理関数の積分とそれに帰着できるもの
10.広義積分とベータ関数,ガンマ関数
10.1 広義積分の収束の判定
10.2 ベータ関数とガンマ関数
11.積分の応用
11.1 曲線の長さ
11.2 級数の収束
11.3 テイラー展開
12.多変数積分法
12.1 リーマン積分の定義
12.2 累次積分の公式
12.3 面積確定領域
12.4 一般の領域における重積分
13.重積分における変数変換
13.1 変数変換の公式
13.2 逆写像の定理
13.3 ヤコビアンと面積比
13.4 重積分における変数変換の公式
13.5 広義積分
14.線積分とグリーンの定理
14.1 部分積分と線積分
14.2 グリーンの定理とその応用
付録1 実数と数列
付録2 n 次元ユークリッド空間
付録3 リーマン積分と連続関数の積分可能性
問・演習問題の解答とヒント
索引
|
|

江尻 典雄
えじり のりお
1953年 茨城県出身.茨城大学理学部卒業,東京都立大学大学院理学研究科博士課程単位取得満期退学.東京都立大学助手,名古屋大学講師・助教授,名古屋工業大学を経て現職.主な著書に『理系の基礎数学 線形代数学』(学術図書出版)などがある.
三宅 正武
みやけ まさたけ
1946年 愛知県出身.名古屋大学理学部卒業,京都大学大学院理学研究科修士課程修了.金沢大学助手,筑波大学講師,名古屋大学助教授・教授などを歴任.主な著書に『理系の基礎数学 微分積分学』(共著,学術図書出版)などがある.
(情報は初版刊行時のものから一部修正しています)


初等 微分積分学
(改訂版)

微分積分講義

微分積分学

微分積分学
微分積分 主要教科書一覧
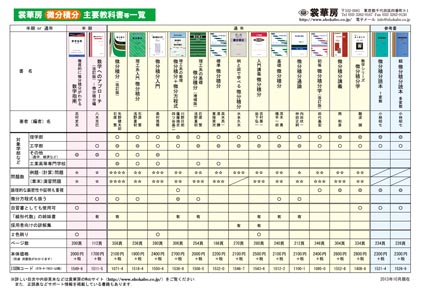
(2013年10月作成,pdfファイル)











|
