|


(Sample Pages)


(Link to Sales Site)
※It takes time to make to order. Also you can not cancel your order.
※POD版のご注文は、お近くの書店・大学生協書籍部、または直接 弊社にお願いします。
※受注生産のため、ご注文されてからお手元に届くまでに時間がかかります(通常 半月程度)。
※ご注文の取り消し・キャンセル、またご注文商品の返品は一切できません。
※以上 あらかじめご了承の上、ご注文くださいますようお願いいたします。

(Link to e-book Sales Site)
・Amazon Kindle ストア
・楽天Kobo
・Google Play
・BOOK☆WALKER
・BookLive!
・紀伊國屋 kinoppy
・セブンネットショッピング
・Reader Store
・ひかりTVブック
・honto
・eBookJapan
・dブック
・どこでも読書
・いつでも書店
・COCORO BOOKS
・ヨドバシ.com
・auブックパス
・DMM電子書籍

|
|
Introduction to Calculus in English[Print-on-Demand]
−英語で学ぶ微分積分学−[POD版]

Authors
九州大学准教授 Ph.D. ヤン・ブレジナ
東京工業大学名誉教授 工博 柳田英二 共著
Bibliographic Information
B5判/286頁/定価4180円(本体3800円+税10%)/POD版 2019年3月発行
ISBN 978-4-7853-0641-0 C3041
.gif)
※本書は,POD版(オンデマンド版)および電子書籍のみの発売になります.※
This textbook is for anybody interested in understanding the basic elements of university calculus.
An English speaker (staying in Japan) who wants to learn "Japanese" calculus can find it here in English and even get acquainted with the Japanese mathematical jargon. If you want to study mathematics in Japan, this textbook will make your first steps a piece of cake! No matter who you are, whenever new terminology appears you can learn it here in both English and Japanese. The text contains furigana (Japanese reading aid) for each new kanji (Japanese character) to ensure a gentle progress.
The textbook is divided into two main parts. Part I is the "computational" one. It contains a revision of "high school" calculus for functions of a single variable and it then focuses on a "quick" application of calculus in several variables. In particular, we give the "know-how" to differentiate and integrate functions differentiate of several variables. Part II is the "theoretical" one. We give a rigorous mathematical explanation of the solution to each of the elementary questions that we treated as "obvious" in Part I. In particular, we show what limit, derivative and integral "really" mean.
微分積分学を英語で学びたい人のための教科書.“標準的な”日本の教科書の“アメリカ”英語版であり,キーワード,定義,定理の日本語訳が簡単に参照できるようになっている.将来,研究者になること,あるいは海外留学を考えている学生にとっては,最初の一冊として最適だろう.
本書は大きく二つの部分からなる.第I部は“計算”の部分で,これは1変数関数に対する“高校”の微分積分の復習に加え,多変数の微分積分をすぐに使えるようになることに焦点を合わせた.つまり,多変数関数を微分し積分するための“技術”を提供する.第II部は“理論”の部分で,第I部で“明らか”として扱ったすべての基本的な問いに対して,厳密な数学的説明を与える.つまり,極限,微分,積分とは“本当は”どのようなものであるかを示す.
※オンデマンド出版書籍(POD版;オンデマンド版)は出版物をデジタルデータ化して,1冊から印刷・製本・販売を行う書籍です.
Information to Assist(サポート情報)
◎ Solutions to selected problems(問題解答) (pdfファイル,2019/3/25現在)
◎ Preface(まえがき) (pdfファイル)
◎ Index(索引) (pdfファイル)
◎ Corrections(正誤表) (pdfファイル)
Contents(目次) (章タイトル) → 詳細目次
Part I Elementary Calculus
1.Calculus in a single variable
2.Differential calculus in several variables
3.Integral calculus in several variables
Part II Foundation of Analysis
4.Sets, points and real numbers
5.Limit and continuity
6.Differentiation
7.Series
Preface(まえがき) (pdfファイル)
Part I Elementary Calculus
1.Calculus in a single variable
1.1 Elementary concepts
1.2 Differentiation
1.3 Primitive function
1.4 Riemann integral
2.Differential calculus in several variables
2.1 Limit and continuity
2.2 Partial derivatives
2.3 Higher order partial derivatives
2.4 Chain rule
3.Integral calculus in several variables
3.1 Integration over bounded sets
3.2 Multiple and iterated integrals
3.3 Transformation of variables
3.4 Improper Riemann integral
3.5 Applications of Riemann integral
Part II Foundation of Analysis
4.Sets, points and real numbers
4.1 Finite and infinite sets
4.2 Infinite sequences of points
4.3 Completeness of real numbers
5.Limit and continuity
5.1 Limit
5.2 Continuity
5.3 Properties of continuous functions
6.Differentiation
6.1 Differentitiation (single variable)
6.2 Indeterminate forms
6.3 Taylor's Theorem
6.4 Differentiation (several variables)
6.5 Local extrema (several variables)
6.6 Implicit Function Theorem
6.7 Constrained extrema
7.Series
7.1 Series of numbers
7.2 Infinite sequences of functions
7.3 Series of functions
7.4 Power series
7.5 Taylor series
Appendix
Darboux integral
Index
|
|

(About the Authors)
ヤン・ブレジナ
Jan Březina
九州大学基幹教育院自然科学理論系部門准教授。専門は偏微分方程式論。
柳田 英二
Eiji Yanagida
やなぎだ えいじ
1957年 富山県に生まれる。1984年東京大学大学院工学系研究科博士課程修了。金沢工業大学講師、宮崎大学助教授、東京工業大学助教授、東京大学助教授、東北大学教授、東京工業大学教授などを歴任。専門は非線形数理、微分方程式。主な著書に『反応拡散方程式』(東京大学出版会)、『常微分方程式論』(共著、朝倉書店)などがある。
(情報は初版刊行時のものから一部修正しています)

(Book by Prof. Yanagida)

数学のとびら 解析入門
(Introduction to Analysis)

理工系の数理
数値計算
(Numerical Computation)
微分積分 主要教科書一覧
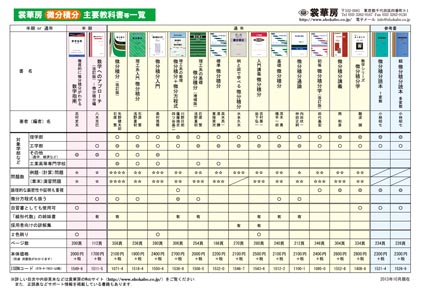
(2013年10月作成,pdfファイル)











|
