|



Amazon
楽天ブックス
セブンネットショッピング
Knowledge Worker
紀伊國屋書店
ヨドバシ・ドット・コム
ローチケHMV
e-hon
Honya Club

丸善,ジュンク堂書店,文教堂
紀伊國屋書店(新宿本店)
三省堂書店
有隣堂
くまざわ書店
コーチャンフォー


|
|
 微分積分入門 −1変数−
微分積分入門 −1変数−
Introduction to Calculus −One Variable−

山形大学 数理科学科 編
A5判/212頁/定価2530円(本体2300円+税10%)/2004年10月発行
ISBN 978-4-7853-1535-1 (旧ISBN 4-7853-1535-0)
C3041
講義中に演習問題を解く時間を作りながら1年で余裕をもって学べる教科書。
学生の数学的素養の多様化に対応して、従来は簡潔に記述するか省略する場合も見受けられた高校課程に含まれる内容も取り上げ、高校で十分学習できなかった読者にも理解しやすいように記述した。
微分積分が専門教育の基礎となることを念頭に、広義積分、定積分の近似計算、フーリエ級数についての節を設け、整級数の項別積分・項別微分、基本的な常微分方程式の解法についてもふれてある。
練習問題・補充問題には42ページの紙数を割いた丁寧な解答をつけた。
サポート情報
◎ 正誤表 (pdfファイル)
1.数列と関数の極限
2.微分係数と導関数
3.三角関数とその導関数
4.指数関数と対数関数
5.関数の増減と平均値の定理
6.高次導関数と関数の展開
7.連続関数の定積分
8.不定積分
9.積分の応用
10.広義積分
11.定積分の近似計算
12.数列と級数
13.フーリエ級数
14.微分方程式
はじめに
1.数列と関数の極限
区間
数列とその極限
級数
関数とその極限
連続関数
左側極限値・右側極限値
2.微分係数と導関数
平均変化率と接線
微分可能性
微分係数
微分可能性と連続性
関数の和・差・積・商などの微分
合成関数の微分法
逆関数とその微分法
導関数
3.三角関数とその導関数
ラジアンの定義と円周率π
三角関数の定義
三角関数の微分
三角関数の逆数関数と逆関数
4.指数関数と対数関数
巾指数と指数法則の拡張
指数関数
数列の極限としての \(e\)
指数関数の逆関数としての対数関数
対数関数の基本的性質
指数関数と対数関数の微分
対数微分
双曲線関数の定義と性質
5.関数の増減と平均値の定理
ロルの定理
平均値の定理
コーシーの平均値の定理
不定形の極限値
関数の増減と極値
極大と極小
6.高次導関数と関数の展開
2次導関数と関数の凹凸
高次導関数
テーラーの定理とマクローリンの定理
テーラー展開とマクローリン展開
7.連続関数の定積分
区分求積法
連続関数の積分可能性と定積分の性質
原始関数と不定積分
8.不定積分
不定積分
置換積分
部分積分
有理関数の積分
\(\sqrt{ax^2+bx+c}\) を含む関数の積分
9.積分の応用
図形の面積
回転体の体積
曲線の長さ
極座標表示された図形の面積
10.広義積分
有限区間上の広義積分
無限区間上の広義積分
広義積分の収束判定定理
ベータ関数
ガンマ関数
11.定積分の近似計算
中点公式
台形公式
シンプソンの公式
近似の誤差
12.数列と級数
級数
絶対収束・条件収束
整級数
項別積分・項別微分
13.フーリエ級数
三角関数の直交性
三角多項式
フーリエ係数とフーリエ級数
三角多項式による近似
リーマン‐ルベーグの定理
一意性の定理
区分的に連続および区分的に滑らか
フーリエ級数による関数の再現
フーリエ級数の応用例
14.微分方程式
微分方程式
微分方程式の例
変数分離形
1階線形微分方程式
関数の一次独立
定数係数2階線形微分方程式
補充問題
付録
導関数表
原始関数表
三角関数の公式
ロピタルの定理に関して
定理12.4(リーマン)の証明
解答とヒント
索引
|
|

山形大学 数理科学科
やまがただいがく すうりかがくか
1949年 山形大学開校、文理学部として数学専攻が設立。1967年 理学部数学科に改組、1995年 理学部数理科学科に改組。
学科のWebサイト
http://www-sci.yamagata-u.ac.jp/math/
(情報は初版刊行時のものから一部修正しています)


数学へのアプローチ
(改訂版)
−微分積分編−

徹底的に微分積分がわかる
数学指南

微分積分通論

微分積分(改訂版)
微分積分 主要教科書一覧
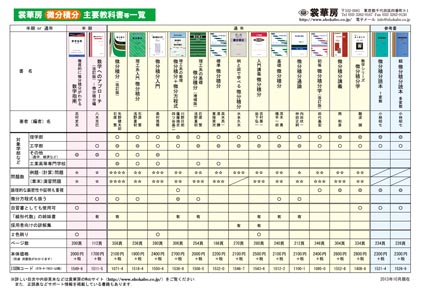
(2013年10月作成,pdfファイル)











|
