第9回 ラマヌジャン
谷口 隆
|
ラマヌジャン（$1887$−$1920$）という，とびきりの異彩を放つインド人数学者がいる．正規の専門教育を受けないまま独力で数学を学び，欧州の数学界を震撼させる独創的な公式を溢れるように生みだした．数学の発展に与えた影響も計り知れない．ところが公式の着想を問われると，本人は「夢の中で女神ナマギーリが教えてくれる」と答えていたらしい．今回はこの伝説と謎の多い数学者，ラマヌジャンのことを著者の力量の範囲で紹介してみたい．
|
|
ラマヌジャンの生誕 $75$ 周年を記念した切手
（"MacTutor History of Mathematics archive" のサイトより転載．）
|
◇ ◇ ◇
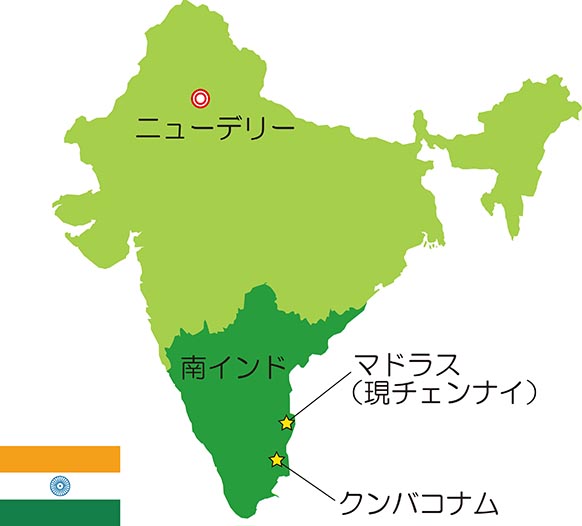
神戸の繁華街から少し北に歩いたところに，「マドラスキッチン」という南インド料理のレストランがある．ナンとカレーの取り合わせという，定番のインド料理は私たち日本人にも馴染み深くなったが，実はそれは北インドの料理だそうだ．マドラスキッチンに行くと，普段見かけない，異国情緒の漂う料理に出会うことができる．ナンはドサという食べ物に代わり，カレーも，種類も味も違っている．
インド出身の友人にこのことを聞いてみたら，「北インドと南インドでは，気候も文化も食事も，いろいろなものが随分違うよ」と教えてくれた．考えてみれば，国土も日本の $9$ 倍ほどあるし，人口も $10$ 億人以上だから，「インド」という国名だけでひとくくりにできないのは当たり前なのだろう．特に南インドは，山河に護られ，地理的に隔絶していた歴史を持つ．イスラムの影響を受けていないインド文化の宝庫であり，宗教的感情，
そして超自然的なものへの畏敬の念を色濃く残す風土のようだ．インド人には菜食主義者が一定数いるが，それも南インド出身者に多い．
レストランの名前にある「マドラス」は，南インドの貿易都市の名である．（注：最近この名は，イギリス植民地化以前の都市名チェンナイに戻された．）ラマヌジャンは，マドラスからさらに $300$ キロほど南下した，クンバコナムという小都市の出身である．ラマヌジャンの母は敬虔なヒンズー教徒で，彼は母から，氏神である女神ナマギーリへの深い信仰心を受け継いで育った．
◇ ◇ ◇
幼い頃から天才で名を馳せていた．高度な数学の本をどんどん読み， $14$ 歳の頃には，学校の先生もラマヌジャンの話はほとんど分からなくなっていたらしい．学校の成績優秀賞に何度も輝き，数学の賞の表彰式で校長に「もしできることなら最高点より上の点をつけてやりたい」と全校生徒の前で紹介された．
$16$ 歳になるかならないかという頃，ラマヌジャンに転機が訪れる．ある日，『数学要覧』という厚手の公式集に出会った．それまではどの科目も勉強する優等生だったが，これ以降，文字どおり右も左も分からなくなるほどこの本に没頭するようになる．ほどなくして英語の試験に落第，奨学金を打ち切られて大学中退へと追いやられた．決して望んだ退学ではなく，彼はこの経歴を不名誉と考え長く気にするのだが，本人としても全く自制が効かなかったというのが真相らしい．「女神が数学を教え始めた」というのもこの頃からである．その後もただただ一人で数学に明け暮れること $5$ 年，かつての神童は，学位も職もなく，世間的にはすっかり人生の落伍者の体であったという．それでもささやかな庇護者に巡り合って，生活費を支給してもらいながらさらに数年，マドラスで研究を続けた．
◇ ◇ ◇
ラマヌジャンは決して，自分の研究の話相手を探さなかったわけではない．ただ，独特のスタイルとあまりの飛び抜けた水準に，理解できる者がいなかったのだ． $25$ 歳のときようやく，ラマヌジャンの送った手紙がケンブリッジ大の若き指導的数学者，ハーディの目に留まる．ラマヌジャン本人が発見したとして記してある $120$ ほどの公式のうち，一部分は高級ではあっても既に知られていたもの，そのほかの一部分はなんとか見当がつくものだった．しかし残りの一部は，ハーディにとっても見たことのない，全く新しい種類のものだった．「初めて目にしたこれらの定理が最高クラスの数学者にしか想像し得ないことは一目瞭然でした．」ハーディはこのときの衝撃をそう説明し，こう付け加えている．「これらは正真正銘の公式に違いない．仮にそうでないとして，いったい誰がこんなものをでっちあげるだけの想像力を持ちえるというのか．」
『数学要覧』との出会いから $10$ 年，ラマヌジャンは前人未踏の領域を女神ナマギーリとただ一人歩み，彼方まで切り開いていたのだ．ハーディはラマヌジャンをケンブリッジに招こうとする．国を離れることはカーストの戒律により禁止されていたのだが，ある夜，ラマヌジャンの母の枕元にナマギーリが立ち渡英の許可が下りる．翌 $1914$ 年，ラマヌジャンはイギリスの土を踏んだ．
◇ ◇ ◇
ケンブリッジの数学者がラマヌジャンと話して驚いたのは，正しいと考えている自分の公式をラマヌジャンが往々にして『証明』できないことだった．「彼の研究成果は，論証と直観と帰納法が奇妙に混交した思考プロセスから得られており，当人でも論理的に首尾一貫した説明ができませんでした」── ハーディはそう述懐している．これこそ正規の専門教育を受けなかったために起きた事態で，不運なことであったかもしれない．しかしハーディは，ここで退屈な正規の教育をラマヌジャンに与えることは，滔々と湧き出る彼の霊感を枯らしてしまうことになりかねないと考える．そこで，証明への助言は必要最低限とし，これまでどおり定理を創出するよう促した．
こうして，若すぎる病死までの約 $6$ 年間に， $30$ 篇あまりの論文が生まれた．誰にも真似のできない，空前の作品だった．そして没後には，インド時代に発見した膨大な未発表の公式が，自作のノートに残された．ハーディは解読に力を傾注したが，数年たっても精密に分析できたのはごく一部にとどまり，「無尽蔵の未発表内容が今後の分析を待っている」と嘆息する破目になった．
ラマヌジャンの病気については現在でもいくつかの説があるようだ．いずれにしても，渡英後すぐに始まった第一次世界大戦が災いしたのは間違いない．厳格な菜食主義者であったラマヌジャンは食料調達に不自由をきたした．暖房燃料も不足し，イギリスの冷気が南国育ちのラマヌジャンを蝕んだ．それで， $1917$ 年頃からは療養所暮らしとなる．病院食を巡って医者と諍いになった．故郷に還すことも検討されたが，戦時下の航海は危険だったし，またインドでもどのみちほとんどの医者は戦争に駆り出されていたため，断念された．戦争が終わってからマドラスに戻るが体調は回復しなかった．病床においても驚くべき創造力を発揮し，時代を遙かに先取りする公式を発見したが，帰国の翌年，女神のもとに召された．
◇ ◇ ◇
ラマヌジャンが書き遺した公式に証明をつける作業は，没後 $100$ 年近くが経つ近年，ようやくほぼ完了した．それでも，証明に携わった数学者は「公式が与えられてそれを証明する作業だからまだ進められたが，当時の数学の水準でどうすればこのような式に思い至れるのかは説明が見当たらない」とこぼしている．ラマヌジャンの研究成果は数学の流れに大きな影響を与え， $1980$ 年頃からは物理法則の記述にも用いられるようになって広い関心を呼んでいる．それでも，どう体系づければよいか未だに判然としない研究も少なくない．
それはひょっとするとラマヌジャンの数学が，論理学や哲学と根っこのところで不可分なギリシャ - ヨーロッパ式の数学の枠組みには，結局のところうまく収まりきらないということなのかも知れない──ラマヌジャンのことを調べているうち，ふとそんな思いに誘われた．ラマヌジャンにあっては数学は，論理学や哲学より，神学や信仰との方が遙かに親近性が高かった．ケンブリッジでは暖炉を囲んで「 $0$ は絶対実在を，無限 $\infty$ はその多様な顕在化を，そして両者を掛け合わせた積 $0\times\infty$ はあらゆる数を表象し，そのひとつひとつが創造の営みに対応している」と熱っぽく語り，周囲の研究者に「神についての思索を表現しない方程式は僕にとっては無価値だ」と話していた．占星術や夢占いにも強い関心を持ち続けた．
◇ ◇ ◇
現在はインターネットが発達して，少年ラマヌジャンを虜にした『数学要覧』も簡単に見ることができる．この公式集を書いたのはジョージ・カー（$1837$ − $1914$）という人物だ．カーはケンブリッジで，数学科の大学生が卒業時に受けるトライパス（tripos）という難試験の家庭教師を生業にしていた．新しい数学の定理を見出す研究者としては第一線では活躍できないと感じたカーは，この仕事を天職と考えて情熱を注いだそうだ．『数学要覧』は，彼の長年の経験と知恵が詰まったトライパス受験対策の参考書なのである．この整理の行き届いた本は簡潔を旨とし，ほとんどの公式は証明がなく，あったとしても要点が僅かに示される程度であった．
当時，トライパスは過熱の一途をたどっていた．その突破が目標の本国イギリスでは，数千もの公式がぎっしりと並ぶ『数学要覧』は苦行難行の象徴となっていたのかも知れない．しかし，この本はとても巧妙に叙述されている．淀みない流れで公式が続き，論理展開が明解で魅力的なのだ．トライパスと無縁の天才数学少年にとって，『数学要覧』の内容を徹底的に吟味することは，この上ない研究テーマとなったのかも知れない．カーとラマヌジャンの，世代，立場，そして国境を越えた稀有な交流も，数学史に残る逸話なのだろう．
【参考文献】
本稿にあるほとんどのエピソードは［$1$］に基づいている．また，［$2$］の視点も参考にした．［$1$］はラマヌジャンの詳細な伝記であり，イギリスで昨年，映画化もされた．［$3$］は『数学要覧』の原著である．（オンラインで無料で閲覧できる．）
［$1$］ 『無限の天才』（"The Man Who Knew Infinity"，ロバート・カニーゲル著，田中靖夫訳，工作舎）．
［$2$］ 『異説 数学者列伝』（森 毅著，ちくま学芸文庫）．
［$3$］ "A Synopsis of Elementary Results in Pure and Applied Mathematics"，George Shoobridge Carr，Cambridge University Press．
（2016/5/11掲載，5/12一部変更，6/24追加画像掲載）
（イラスト：マエカワアキオ）
※ 次回（第10回）は6月1日（第１水曜日）に掲載いたします．どうぞお楽しみに！
ご感想を電子メールでお送りいただければ幸いです．送付先アドレス info@shokabo.co.jp
「数学者的思考回路」 Copyright(c) 谷口 隆，2016
著作権法上の例外を除き，無断で本Webページの全部または一部を転写・複製等することはできません．
（→ 【裳華房】Webサイトのご利用について）
|
