【コラム：数学者的思考回路】（13）ピタゴラスの定理・証明コレクション

第13回　ピタゴラスの定理・証明コレクション

谷口　隆　　　　

　直角三角形において，斜辺の長さを $c$，他の $2$ 辺の長さを $a$， $b$ とすると $a^2+b^2$ ＝ $c^2$ が成り立つ．ご存知三平方の定理，いわゆるピタゴラスの定理だ．

江戸時代，日本では勾股弦（こうこげん）の定理と呼ばれていた．
　今日では，ピタゴラスの定理には数百にも及ぶ証明が知られている．今回はそのような中から何通りかを紹介し，それぞれの特徴についても考えてみたい．証明については図に加えて大まかな方針を書くので，細部はぜひご自身で考えていただけたらと思う．以下では上図のように，斜辺は ${\rm AB}$ であるとし，また辺の長さは ${\rm BC}$ ＝ $a$， ${\rm CA}$ ＝ $b$， ${\rm AB}$ ＝ $c$ としよう．

1．『原論』の証明

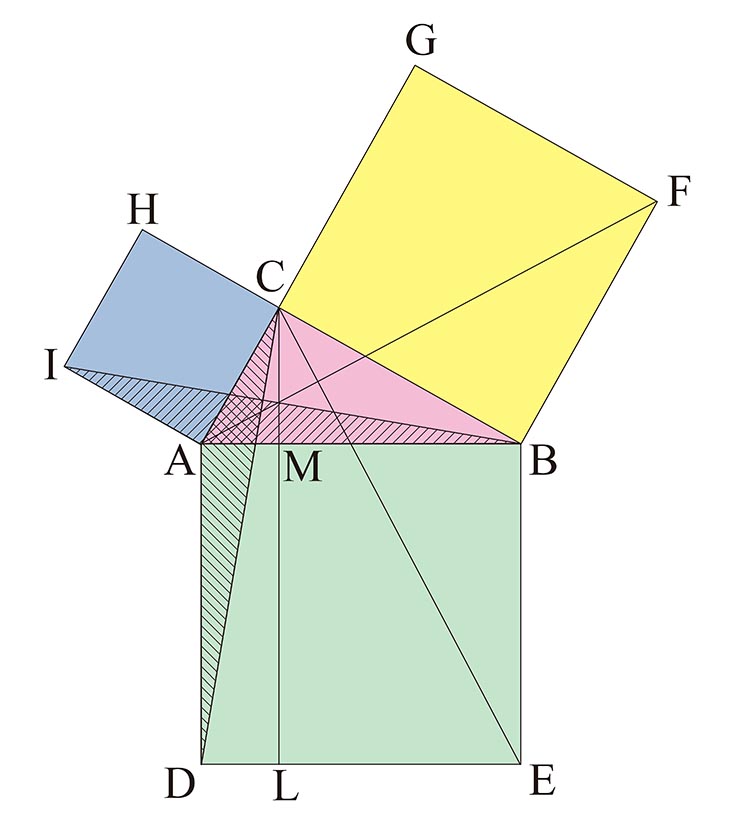　まずは古式ゆかしいユークリッドの『原論』にある証明を．直角三角形の各辺に正方形を描こう．黄色，青色，緑色の正方形の面積は，それぞれ $a^2$， $b^2$， $c^2$ である．黄色と青色の面積の和が，どうして緑色の面積になるのか，という問題になる．
　ポイントは，斜線を引いた $2$ つの三角形（ $\triangle {\rm IAB}$ と $\triangle {\rm CAD}$ ）が合同になること．これを使って考えると，青色の面積が，長方形 ${\rm ADLM}$ の面積と等しいことが示せる．（ $\triangle {\rm IAC}$ の面積と $\triangle {\rm IAB}$ の面積が等しいことに注意．）
　図形の右側部分も同様に考えて，黄色の面積は，長方形 ${\rm BELM}$ の面積と等しい．
　$a^2$ とあれば，それが一辺の長さが $a$ の正方形の面積だと考えるのは自然な発想だろう．この証明には，短さや巧みさよりも，正方形の面積の和 $a^2+b^2$ がなぜ再び正方形の面積 $c^2$ になるのかをなるべく明瞭に説明したい，そんな意図が込められているように感じられる．

2．面積を計算する証明

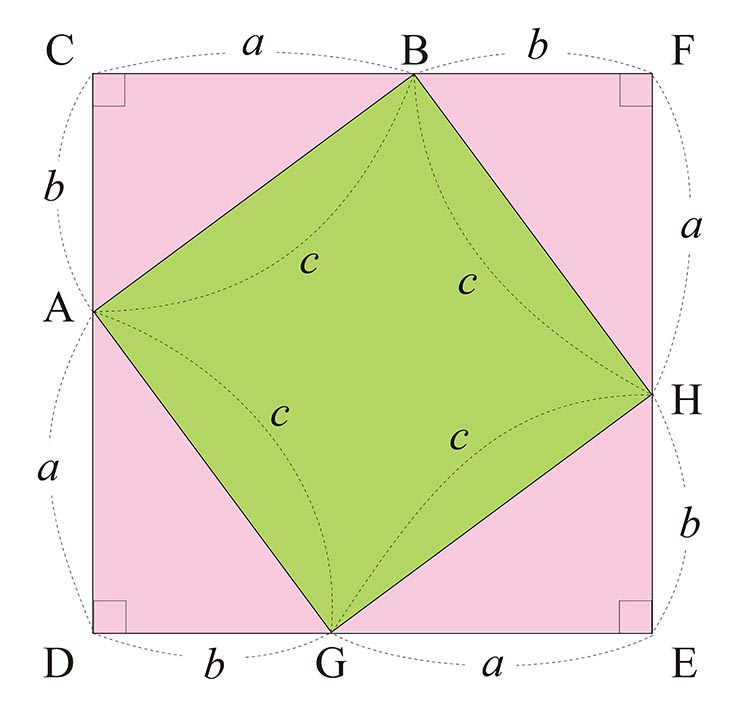　当初の直角三角形 ${\rm ABC}$ と同じものを計 $4$ 枚用意して，図のように配置しよう．${\rm CAD}$， ${\rm DGE}$， ${\rm EHF}$， ${\rm FBC}$ がそれぞれ一直線上に並ぶように置く．そうすると，外側の四角形 ${\rm CDEF}$ は一辺が $a+b$ の正方形だ．したがってその面積は $(a+b)^2$ である．
　今度は内側の四角形 ${\rm AGHB}$ に注目してみよう．少し考えると，この四角形はどの角度も直角と分かる．つまりこれは，一辺の長さが $c$ の正方形なのだ．このことから，正方形 ${\rm CDEF}$ の面積を，もう一つ別の式で表すことができる．
　証明は短いが，$\triangle {\rm ABC}$ のコピーを計 $4$ 枚も用意して内外に正方形を $2$ 個作るなんて，言われないとなかなか思いつけないだろう．巧みな証明だ．

3．相似比を使う証明

　相似な図形があれば，面積比はその相似比の $2$ 乗になる．このことを使った証明方法がある．
（ピザを注文するときにウッカリしていると失敗するアレである．Ｍサイズは直径 $25$ cm，Ｌサイズは直径 $35$ cmと書いてあるのを見て「あぁ， $1.4$ 倍か」と思ってＬを注文したら，Ｍの $2$ 倍ほどのボリュームのピザが届いて大変な思いをしたことが私もあった．そのときはしみじみと $1.4^2$ ＝ $1.96$ ≒ $2$ を思った．）
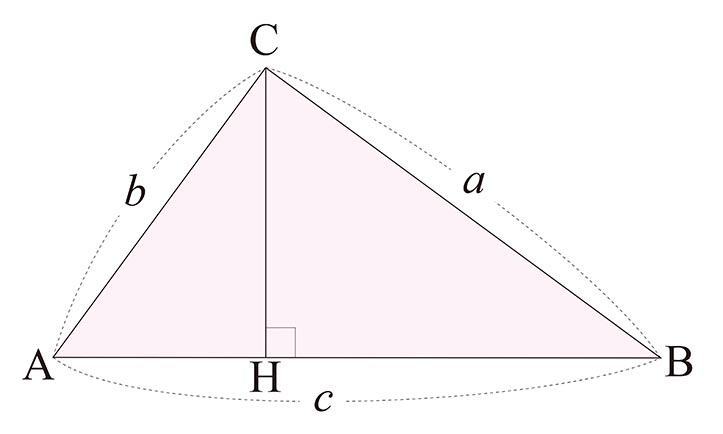　さて， ${\rm C}$ から ${\rm AB}$ に垂線 ${\rm CH}$ をおろそう．このときできた $2$ つの三角形 $\triangle {\rm CBH}$， $\triangle {\rm ACH}$ はもとの三角形 $\triangle {\rm ABC}$ と相似である．どれも直角三角形で，斜辺の長さは順に $a$， $b$， $c$ だから，面積比は $a^2$ ： $b^2$ ： $c^2$ である．ところで $2$ つの三角形 $\triangle {\rm CBH}$ と $\triangle {\rm ACH}$ の面積の合計はもちろん $\triangle {\rm ABC}$ の面積だ．したがって $a^2+b^2$ ＝ $c^2$ である．
　ピタゴラスの定理がどうして成り立つのか，その理由はこれがいちばん「分かりやすい」かも知れない．

4．面積を計算する証明その２

　面積計算による証明をもう一つ紹介しよう． $\triangle {\rm ABC}$ と合同な三角形 $\triangle {\rm EDC}$ を用意して，${\rm ACD}$ が一直線となるように置く．
　楔（くさび）のような形をした四角形 ${\rm DAEB}$ の面積を考えてみよう．これは二つの直角二等辺三角形からできていて，面積は $\dfrac{a^2}{2}+\dfrac{b^2}{2}$ である．ところでこの図をよくよく見つめると，実は ${\rm AB}$ と ${\rm DE}$ は垂直であることが分かる．そのことから，四角形 ${\rm DAEB}$ の面積のもう一通りの計算方法が得られる．お考えいただきたい．
　この証明も， $\triangle {\rm ABC}$ と$\triangle {\rm EDC}$ の巧妙な配置がポイントだと思う．

5．内接円を使う証明

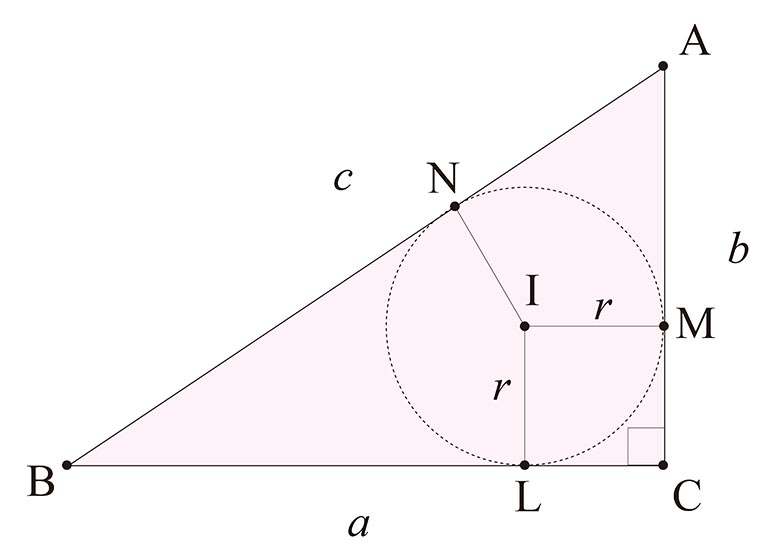　内接円の半径を $r$ としよう． $\triangle {\rm ABC}$ の面積は $\dfrac{1}{2}ab$ だが，これを内心 ${\rm I}$ と各頂点を結ぶ $3$ 本の線分で $3$ 分割して求めると， $\dfrac{1}{2}(a+b+c)r$ でもある．したがって $(a+b+c)r$ ＝ $ab$ が成り立つ．
　一方で，図をよく見ると

　・${\rm AN}$ ＝ ${\rm AM}$， ${\rm BN}$ ＝ ${\rm BL}$
　・四角形 ${\rm ILCM}$ は正方形

が分かって，ここから $a+b$ ＝ $c+2r$ が得られる．さて， $2$ つの式から $r$ を消去してみると $･･･$ ？
　補助線ならぬ「補助円」を使った証明で，どうしてこんなことで証明できるのか，ちょっと不思議な気持ちになる．でも，やっぱり証明はちゃんとできている．この証明を変形すると，傍接円を使った証明も作れる．

　お気に入りの証明はあったでしょうか．一番気に入ったのはどの証明でしょう？？

【参考文献】

　ピタゴラスの定理の証明を集めた本は多数あるが，今回の記事を書くにあたり，『ピタゴラスの定理 $100$ の証明法 ― 幾何の散歩道』（森下四郎著，プレアデス出版）を参考にした．証明が種類別に分けられ，系統的に説明されていて分かりやすい．考えていて楽しくなるような，趣向を凝らした証明も載っている．興味のある方はご覧いただきたい．